|
|
Table of Contents
RRG Relative Strength
Introduction
RRG Relative Strength is an indicator pair designed to measure relative performance and the momentum of relative performance. JdK RS-Ratio is an indicator used to measure the relative performance of one security against another. Its companion, JdK RS-Momentum measures the momentum of RS-Ratio, which means it measures the momentum of relative performance. RS-Ratio and RS-Momentum are used in Relative Rotation Graphs (RRGs), but this indicator pair can also be plotted on SharpCharts. This article will focus on RS-Ratio and RS-Momentum as indicators on SharpCharts. There is another ChartSchool article detailing their use in Relative Rotation Graphs.
Note: “Relative Rotation Graphs™” and “RRG Charts™” are registered trademarks of RRG Research.
Normalization
RS-Ratio and RS-Momentum are “normalized,” which means these indicators are expressed in the same unit of measure and fluctuate above/below the same level (100). This normalization process means RS-Ratio values for different securities can be compared, as long as the same benchmark is used. For example, chartists can plot the RS-Ratio for each of the nine Sector SPDRs and use the S&P 500 as the benchmark. The sector with the highest RS-Ratio would show the most relative strength, while the sector with the lowest RS-Ratio would show the most relative weakness.
JdK RS-Ratio
RS-Ratio is an indicator that measures the trend for relative performance. Similar to the price relative, RS-Ratio uses ratio analysis to compare one security against another (usually the benchmark). It is designed to define the trend in relative performance and measure the strength of that trend.
The chart below shows the Technology SPDR (XLK) in the main window, the price relative (XLK:$SPX ratio) in the middle window and the RRG indicators in the bottom window. We will focus on RS-Ratio (red) first. RS-Momentum (green) will be covered in the next section.
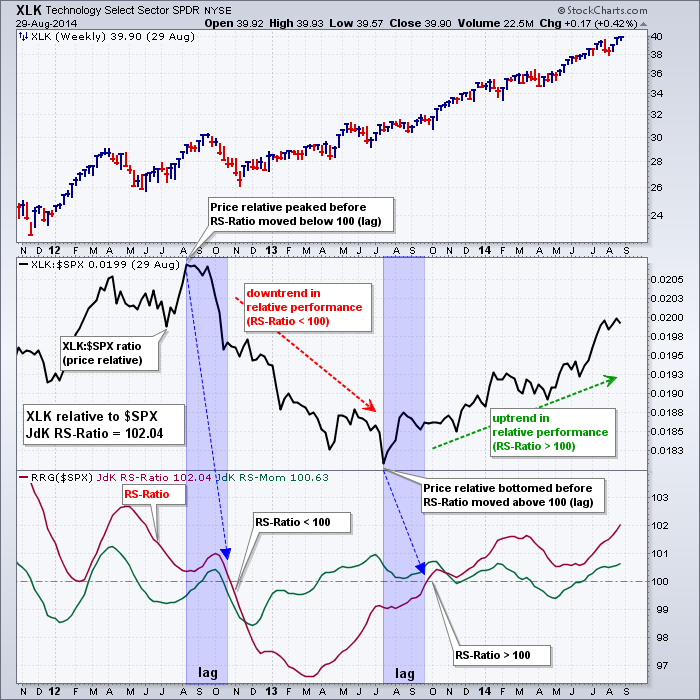
RS-Ratio gives chartists a clear tool to define the trend in relative performance. This indicator reflects an uptrend in relative performance when above 100 (relative strength) and a downtrend in relative performance when below 100 (relative weakness). The further the indicator is above 100, the stronger the uptrend in relative performance. The further the indicator is below 100, the stronger the downtrend in relative performance.
As with all trend-following indicators, such as moving averages, the trend-following model that powers RS-Ratio includes a lag period. This means there will already be upward movement in the price relative before RS-Ratio crosses above 100. Conversely, there will already be downward movement in the price relative before RS-Ratio crosses below 100. Notice on the chart above how the price relative (XLK:$SPX ratio) peaked in early August, but RS-Ratio did not cross below 100 until mid-October. Similarly, the price relative bottomed in mid-July, but RS-Ratio did not cross above 100 until mid-September. This is typical for trend-following indicators that are designed to ignore the blips and focus on the trend. The chart below shows the Consumer Discretionary SPDR (XLY) with another example.
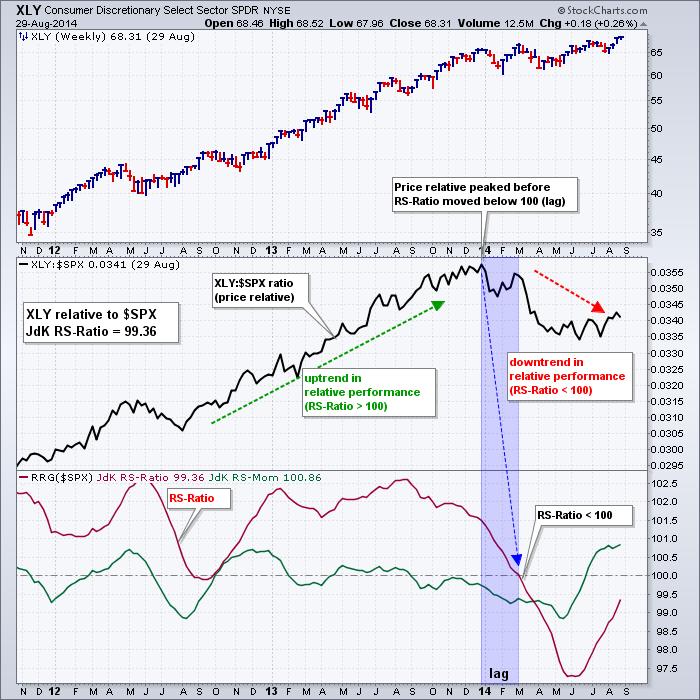
Keep in mind that the values for RS-Ratio can be compared when using the same benchmark security. Let's assume we are comparing relative performance for four Sector SPDRs against the S&P 500 and the RS-Ratio values are as follows: XLK=102.04, XLI=101.41, XLF=100.2, and XLV=103.66. First, all four have RS-Ratios above 100 and this means all four show relative strength (against the S&P 500). Second, XLV shows the most relative strength because its RS-Ratio is the highest of the four. XLF is the weakest of the four because its RS-Ratio is the lowest.
JdK RS-Momentum
Before looking at RS-Momentum in detail, let's review the concept behind momentum and how it relates to trend. As with price charts, chartists should keep in mind that momentum changes course before the trend actually reverses. Not all momentum moves, however, result in trend reversals.
Consider an example using price and a moving average. Price first moves towards the moving average, crossing it if the move extends. Price, however, does not always cross the moving average to signal a trend reversal. Aggressive traders would more likely take a position as price moves towards the moving average because this means momentum is improving. Conservative investors would more likely wait for price to move above the moving average because the trend has not fully reversed.
RS-Momentum is an indicator that measures the momentum (rate-of-change) of RS-Ratio. As a momentum indicator, it leads RS-Ratio and can be used to anticipate turns in RS-Ratio. Typically, RS-Momentum crosses above 100 when RS-Ratio is forming a trough and starting to move up. Conversely, RS-Momentum crosses below 100 when RS-Ratio is forming a peak and starting to move down.
The chart below shows the Utilities SPDR (XLU) with RS-Momentum in green and RS-Ratio in red. RS-Momentum crossed above 100 in mid-December and held mostly above 100 for four weeks. Notice how RS-Ratio bottomed as RS-Momentum moved above 100 and RS-Ratio crossed above 100 later in January.
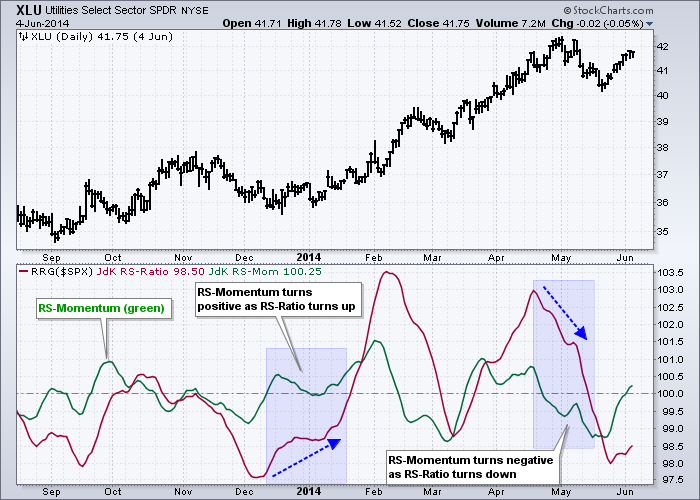
Keep in mind that RS-Momentum is an indicator of an indicator (RS-Ratio). Furthermore, it is a momentum indicator and that means it will move above/below the 100 level often. Chartists may want to focus on sustained moves above/below 100 to anticipate a similar cross in RS-Ratio.
The chart below shows the Biotech SPDR (XBI) with two examples highlighting the relationship between RS-Momentum and RS-Ratio. The gray shading shows RS-Momentum below 100 for four of six weeks in February-March. Even though the indicator popped above 100 briefly, this pop did not last long and quickly moved back below 100. This was a sign that momentum was turning negative for RS-Ratio, which ultimately crossed below 100 in the second half of March.
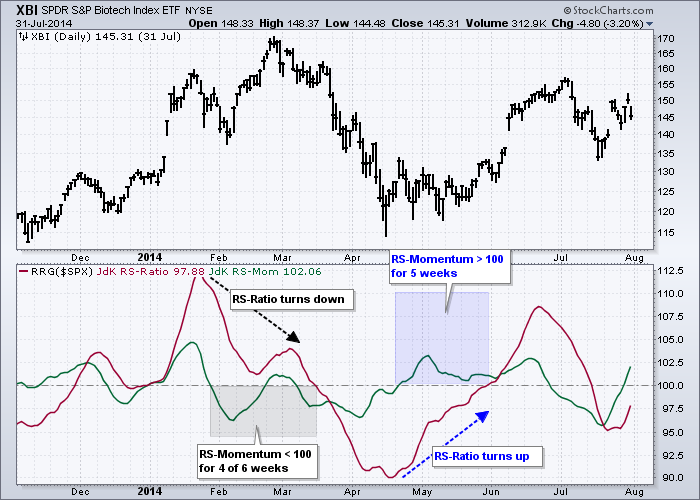
The blue shading shows RS-Momentum above 100 from mid-April until late May. RS-Ratio bottomed as RS-Momentum moved above 100, but did not cross above 100 until the end of May. The cross above 100 in RS-Ratio, by the way, came just before the early June surge in XBI.
Weekly Versus Daily
As with regular bar charts, the chosen timeframe can affect RS-Ratio and result in different conclusions. In the example below, the left chart shows two months of daily data for the S&P 500, where the two-month trend is down. The chart on the right shows one year of weekly data, where the overall trend is clearly up. The yellow shaded area highlights the two months shown on the daily chart to put this decline into perspective. Clearly, this is a short-term downtrend (pullback) within a long-term uptrend.
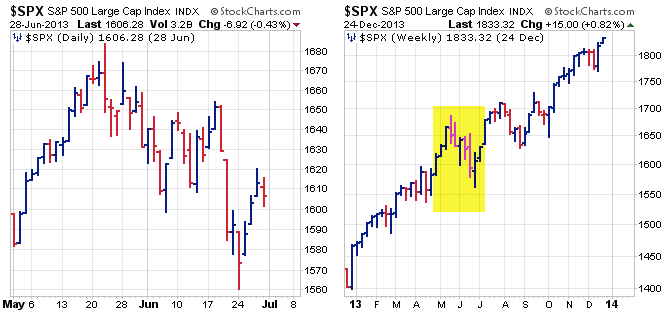
Now let's look at examples using weekly and daily charts for RS-Ratio and RS-Momentum. The first chart uses a weekly timeframe and both indicators are below 100, which indicates a downtrend in relative performance and negative momentum. This weekly chart captures the long-term trend. The second chart uses a daily timeframe and both indicators are above 100, which indicates an uptrend in relative performance and positive momentum. This daily chart captures a smaller trend than the weekly chart.
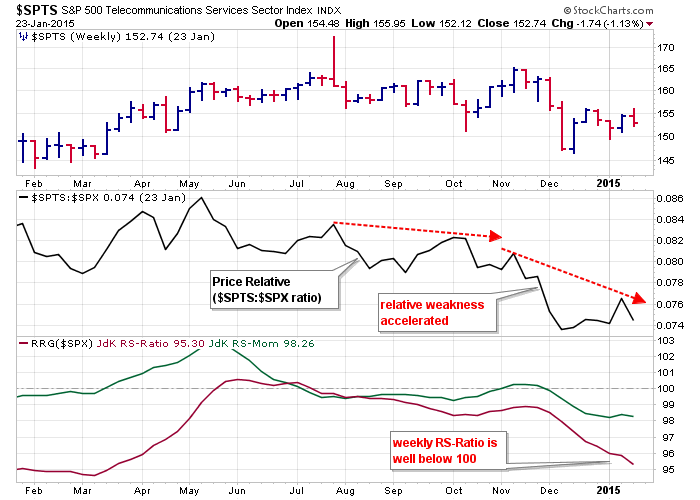
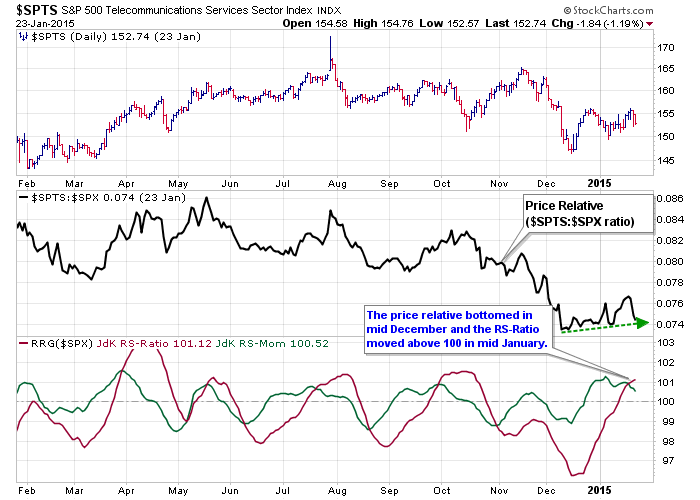
If we assume that the long-term trend is dominant here, then we can also infer that the long-term downtrend in relative performance will ultimately trump the short-term uptrend in relative performance. In other words, the uptrend in relative performance on the daily chart is a mere blip on the weekly chart and not enough to reverse the bigger downtrend in relative performance.
As with all aspects of technical analysis, it is a very good habit to study different timeframes to get a complete picture. The Telecom sector is clearly underperforming on the weekly timeframe and momentum is negative. The upturn in RS-Momentum shows a decrease in negative momentum on the weekly timeframe, and this is reflected on the daily chart where RS-Ratio and RS-Momentum moved above 100.
Conclusion
RS-Ratio and RS-Momentum give chartists a four-pronged approach for measuring relative performance. First, RS-Ratio measures relative performance against another security, usually the benchmark. At its simplest, a security shows relative strength when above 100 and relative weakness when below 100. Second, the RS-Ratio value tells us the degree of relative strength or relative weakness. The further above 100, the more relative strength. The further below 100, the more relative weakness. Third, chartists can compare RS-Ratio values to determine the strongest securities within a group. Fourth, RS-Momentum measures the momentum of RS-Ratio, which can be used to anticipate turns in RS-Ratio. As with all indicators, chartists should combine relative performance with other technical tools to get a complete picture.
Using with SharpCharts
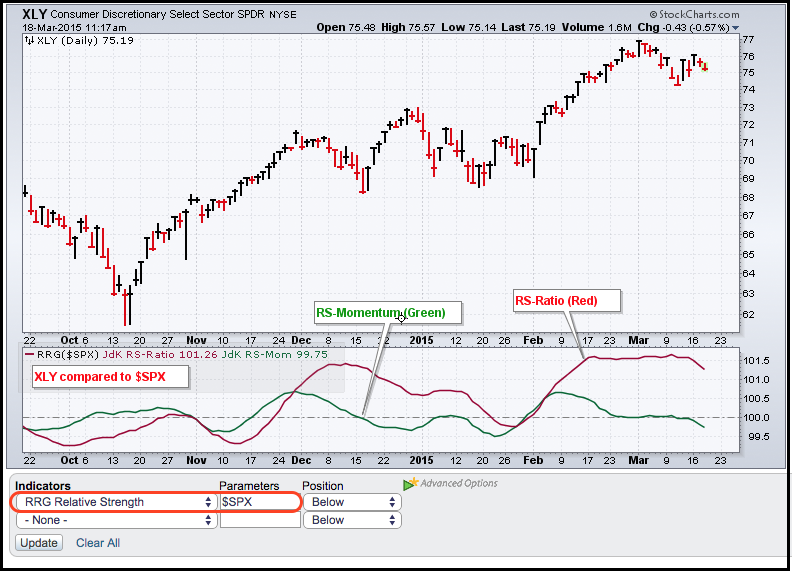
RS-Ratio and RS-Momentum are available as indicators in SharpCharts. They are grouped together as “RRG Relative Strength” in the indicator dropdown list. Once selected, users can set the benchmark security by entering its symbol in the “parameter” box. The example below shows the Consumer Discretionary SPDR (XLY) with the S&P 500 as the benchmark. Keep in mind that any symbol can be used to measure relative performance. If you want to compare the performance of the Consumer Discretionary SPDR (XLY) to the Technology SPDR (XLK), simply enter XLK as the parameter and click update. Click here for a live example of RRG Relative Strength in action.
Frequently Asked Questions
Q: How much data is needed to plot RRG?
A: You need about 50 data points minimum, so more than 50 days of data for a daily RRG. For weekly, you'll need roughly 250 days of data.
